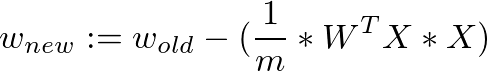梯度下降

昨天我們提到，令我們的函數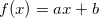為： 則誤差為：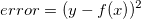
其中 x 為輸入，y 為輸出。我們想要將誤差最小化，因此可以透過微分來求算。

首先，我們先來回想一下微分的定義：

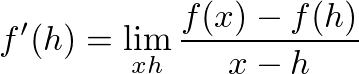
我們希望透過逐步地增加（或減少）a，來看看我們的誤差是不是真的在減少。

在一元方程式當中（只有一個變數），我們可以很容易求算導數，並且讓導數為靈就可以求得最小值與 x 為多少。

可是對於多變數的方程式來說，要怎麼找到導數就變得相當困難，例如在三維空間當中，切面會是一個平面，有無限多條：

更別說在真實的情況當中有幾千個權重了。

顯然之前學到的方式並不能解決我們的問題，因此我們透過偏微分來求算單一個值的微小變化在整個方程式的變化為何。

偏微分的幾何意義是，不關心其他變數（把其他變數都當作常數），只關心單一變數對整個函數的變化。

什麼是梯度？

我們應該如何知道我們選擇的方向是正確的？對於一個二次曲線來說，我們每次都往切線的方向走就對了。而對更多維度的推廣，在數學上有個名詞叫做**「梯度」**。

為了解釋什麼是梯度，首先我們先定義一個函數：

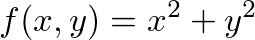
梯度的定義則是對裡頭的每個變數做偏微分所組成的向量空間：

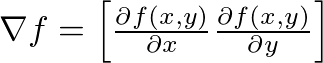
不過這在幾何到底有什麼意義？在二維平面當中，我們可以透過畫圖的方式很快地理解，微分就是函數在某個點上變化的方向。

因此，我們可以把梯度想像成一個指向最低點的指南針，他會告訴你該往哪裡走，順著走總有一天會到達最小值。

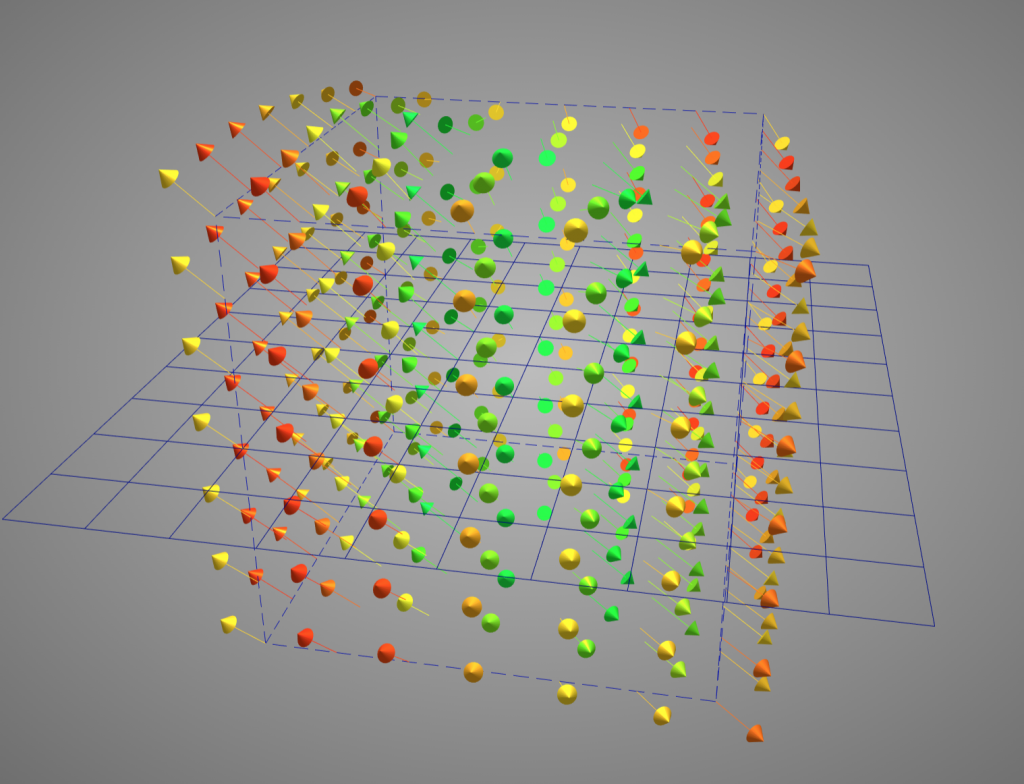
那麼我們該怎麼走呢？梯度下降法給了一個公式，每次計算函數點上面的梯度，並且沿著反方向的步長（step）迭代，總有一天會走到局部最小值。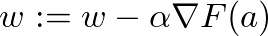

現在已經有了梯度下降的公式，我們可以試著計算一下線性迴歸的梯度下降應該怎麼做：

線性迴歸的梯度下降推導

為了方便等下的微分計算，我們將 error 函數稍作調整：

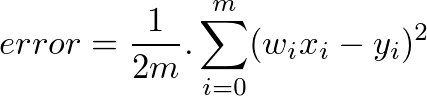
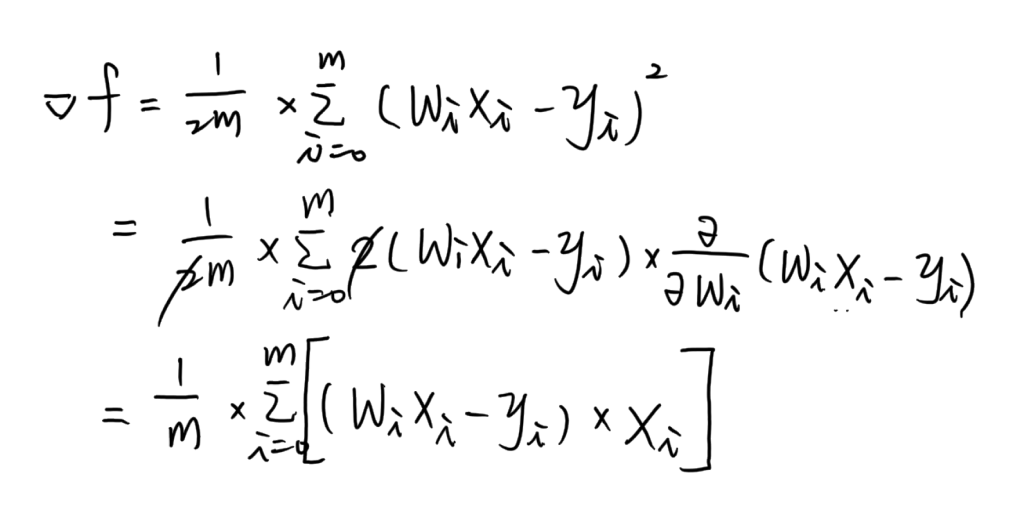
現在我們已經具備訓練一個線性迴歸模型所需要的所有工具了，明天讓我們來試著用歷年的台灣薪資預測看看明年的台灣薪水吧！

注意事項

1. 在這邊的 error 函數有時會叫做成本函數，有時常用 J 來表示
2. 權重通常會用 W，有時會用 ? 表示，只是符號上的不同
3. 在實務上我們會把總合做向量化，所以上面的等式可以化簡為